Review Article - (2024) Volume 10, Issue 1
Social work studies of dermatological health show that prevention is a low cost factor with respect to the treatment of a disease acquired by parasite contamination. In this sense, a documentary, cross sectional and descriptive study was carried out with a non-probabilistic selection of indexed sources, registered in ISSN and DOI, during a period that goes from 2019 to 2022 with the purpose of establishing an integral model for the study. Of an outbreak of dermatological contamination and derive intervention strategies from social work in basic education institutions. The propagation model turned out to be the most complete, although the integration of other models that explain the contagion problem and future treatment, recantation and prevention scenarios is offered. The need to carry out strategies for prevention and promotion of disease free lifestyles, as well as individual self-care and collective co responsibility, is noted.
Governance • Health • Disease • Parasite • Intervention
Until January 2022, the pandemic has killed six million, although governments and health ministry’s recognize an underreporting of 18 million. The number of deaths related to COVID-19 would rise to 24 million. In Mexico, the pandemic has ended the lives of 300,000 recognized by the government but underreporting reaches the figure of 700,000.
The World Health Organization declared that COVID-19 is not transmitted between infants, although cases of infection, illness and death have increased. Governments have followed the WHO recommendation to avoid vaccinating infants, even though the delta and omicron variants have impacted infant health. The ministries of health and education pressed for the return to classrooms and face to face classes without vaccinating students. In January 2022, the WHO recommended the vaccination of infants due to the increase in deaths. In Mexico, the government interpreted the WHO recommendation as avoiding immunizing students [1].
In the framework of deaths from COVID-19, dermatological health has been affected. The public health system, being focused on the SARS CoV-2 coronavirus, has neglected attention to other diseases. In addition, users of the health service have confined themselves to avoid getting infected in hospitals. Users have postponed their treatments. The pandemic also affects the basic education system in which students interrupt their dermatological treatments or cannot access them to avoid getting COVID-19. Dermatological infections and diseases emerge in a context of school overcrowding but distancing and confinement redirect the cycle. Confined and isolated students tend to stress and avoid the daily personal hygiene that school dynamics require of them. Therefore, the parasite epidemic is possible, even when students are confined and isolated [2].
The objective of the present study is to formalize a mathematical model that is closest to the investigation of contamination and interactions of lice with children. Exponential function models, Quetelet logistic models, Locka-Volterra function models, McKendrick propagation models and dermatological treatment models are reviewed to establish an intervention device for the governance of dermatological health in public education institutions. Basic with emphasis on health promotion and self-care in vulnerable groups.
What are the approaches that explain the impact of the pandemic on dermatological health in a scenario of infection and disease due to an epidemic of parasites in children of basic schools in Mexico city?
The premises that guide this work warn: 1) The SARS CoV-2 coronavirus pandemic and the COVID-19 disease can coexist with other infections and dermatological diseases such as parasites; 2) Confinement and distancing of students reduces the chances of infection and illness, but encourages stress; 3) Students with stress levels may avoid personal hygiene, as well as parasite prevention practices; 4) COVID-19 and parasites can coexist in a scenario of confinement and distancing, increasing significantly in the return to face-to-face classes; 5) Basic education systems do not have the resources to prevent both COVID-19 and parasites, delegating the care of students to families; 6) The governance of public health, with an emphasis on dermatological health, can be built on the differences between the rulers and the ruled due to the lack of vaccination and resources [3-5].
Public health governanceThe history of public health, health policies and dermatological programs and health prevention and promotion strategies are areas of multidisciplinary research and knowledge in which social work acquires greater relevance by establishing an approach with vulnerable groups such as infants. It is estimated that the costs of treatment exceed the costs of prevention to a greater extent, since for every peso spent on the treatment of diseases or care for accidents, a penny would be spent on prevention. In this sense, both areas, health promotion and social care for diseases, pandemics or epidemics, are central issues of management and administration in health policies (Figure 1).
Figure 1: Public health governance (comparison data set).
Source: Elaborated with data study.
In other words, the participation of vulnerable groups is increasingly significant to the extent that they develop lifestyles and self-care strategies for their personal and collective health. Precisely, in this phase the dialogue between specialized institutions and citizens is a problematic hinge in the achievement of objectives, elaboration of tasks and obtaining goals in the short, medium, and long term by health professionals in general and professionals of the social work in particular.
In this way, the governance of dermatological health will be understood as a set of policies for the inclusion of governmental and social actors in the face of a public health problem such as dermatological diseases in vulnerable groups. It is a surveillance, follow-up and co responsibility system between the authorities and the potential victims of diseases, epidemics, or pandemics [6,7].
Unlike health policies focused on research, specialization and treatment, dermatological health governance is low cost, includes all actors and establishes co responsibility agreements around objectives, tasks and goals established in a medium term. In such a scenario, the participation of public health professionals and of social workers, is extremely important since the strategies are disseminated in the institutions and sectors most affected by dermatological contamination [8].
Contamination public health
In Mexico, the lice epidemic, year after year, has manifested itself in public and private schools, affecting above all the child population. Insects approximately one to two millimeters long that hides in clothing, bedding, and the scalp. This parasite causes inflammation, itching and sucks the blood of the person who hosts it (Figure 2).
Figure 2: Public health governance (diagraph).
Source: Elaborated with data study.
Lice are brown, oviparous insects that live exclusively on human hair and can be seen with the naked eye (they measure between two and three millimeters). They don't have wings and can't fly, but their six legs, which end in small claws, allow them to hold on tightly to fur. They also have a small head with mouth parts prepared to bite the scalp and suck the blood they feed on [9,10].
A louse lives between 33 and 35 days and goes through three stages:
Nit: For 6–7 days. It is the egg of the louse (an adult female lays and average of 110-150 during her life). It is attached to the base of the hair. Only 60% reach the adult louse. Nits differ from dandruff in that the former present great resistance when trying to be removed and cannot be removed with a simple wash.
Nymph: For 9–10 days. It is the louse just hatched from the egg. It is invisible to the human eye. Its body undergoes three growth molts until it becomes an adult and can reproduce.
Adult louse: For 15–16 days. The females deposit four to eight eggs daily at between one and two millimeters from the scalp.
Her favorite places: The hairs behind her ears, on the crown of her head, and on the back of her head. To ensure their adherence to the hair, they secrete a sticky and water insoluble substance that fixes the nit to the hair shaft.
According to information from the Mexican society of dermatology, in 2019 there is an epidemic in our country, which has manifested itself in public and private schools, and continues to affect the child population of our country. The louse does not discriminate against race or social status and despite the myths of most Mexicans, it is not a matter of poor hygiene, but rather they are spread by contact between people in closed places such as schools, workplaces, families, prisons and hospitals.
State of knowledge: Mathematical models of public health
Exponential function models: The exponential function is present in many growth phenomena: Animal, plant, economic, spread of epidemic diseases and others. In all of them the variable is time. It is also known as unlimited population growth. It serves to describe any process that evolves so that the increase (or decrease) in a small interval of time is proportional to what was at the beginning of it. That is, the rate of change of a population only depends on its size.
•It is reasonable for small populations in large environments.
•Population growth rate is proportional to its size. Graph of a function that satisfies the differential equation
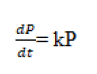
We must take into account the following considerations:
P=Population (dependent variable). t=Time (independent variable).
k=proportionality constant (parameter). Between the rate of population growth and its size.

Here we will treat only ordinary equation
Since it is proportional to the population, it is expressed as the product kP.
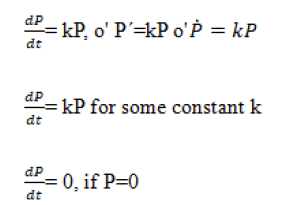
P (t) =0. This solution of a differential equation is called an equilibrium solution.
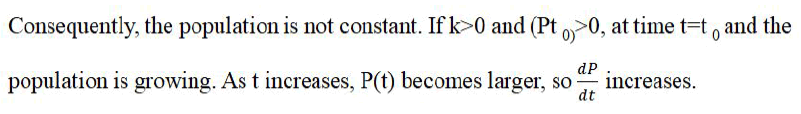
Logistic function model
The logistic function, logistic curve or S-shaped curve is a mathematical function that appears in various models of population growth, spread of epidemic diseases and spread in social networks. Said function constitutes a refinement of the exponential model for the growth of a magnitude. It was the Belgian mathematician, statistician, and astronomer Adolphe Quetelet who in 1835 proposed the idea that population growth was slowed down by a resistance proportional to the square of said population (mechanical hypothesis).
The logistic curve: To fit the exponential population growth model, you must take into account a limited environment and resources.
If the population is small, the rate of population growth is proportional to its size.
If the population is too large to be supported by its environment and resources, the population will decrease. That is, the growth ratio is negative.
Considerations:
t=time (independent variable).
P=Population (dependent variable).
k=growth rate coefficient for small populations (parameter).
We must consider that limited resources must enter another amount. This quantity is a second parameter, denoted by N (it will be called support capacity) of the environment.
In terms of carrying capacity, we assume that P(t) grows if P(t)<N; if P(t)>N is decreasing.
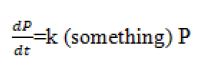
We add "something" close to 1, if P is small
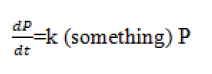
But if we want "something" be negative
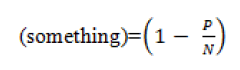
In this way, the logarithmic equation is as follows:
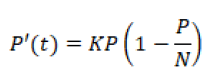
For this work we consider the following.
Where:
P(t): It is the population of prey (children) at the current time.
K: is the growth coefficient of the population of empiojadas.
P: Child population with lice.

What we see in the graph is that as there are outbreaks of lice, and children who are in close contact (given the characteristics of the children), the population of lice will increase continuously.
Lotka-Volterra model
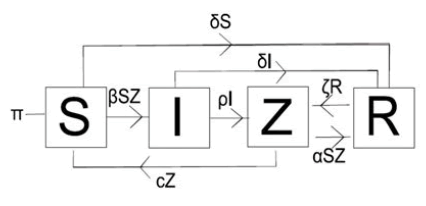
Without a doubt, the mathematical function for calculating future populations that has aroused the most interest is the well-known ones: With the name of exponential, logistic and the Lotka-Volterra model and others. No species lives in isolation and interactions between species provide some of the most interesting models, here is a simple predator prey system of differential equations where one species "eats" the other, in this model we have two time dependent quantities. Our model then has two dependent variables that are both functions of time. In this case we will call the prey “school children” and the predators “lice”, and we will denote the prey S and the predators by P.
Lotka-Volterra growth model, also known as predator prey equations, are a pair of first order differential equations nonlinear that are used for modeling two interacting populations, a prey and a predator. The equations were independently proposed by Alfred J. Lotka in 1925 and Vito Volterra in 1926. Such equations are defined as:
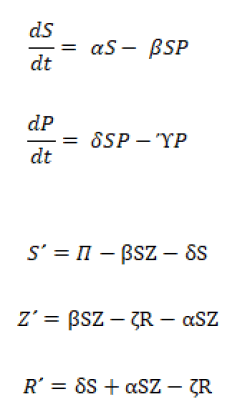
This model is a bit more complicated than the basic SIR models that generally characterize infectious diseases as this model has two mass action transmissions, which leads to having more than one non-linear term in the model. Incidence specifies that an average member of the population makes enough contact to transmit the plague (βN) to others per unit of time or by too close contact, where N is the total population of children in the school (we assume that there is the closest contact). Nearby without lice. The probabilities that a random contact by a lousy person (Y/N), will turn another child lousy, therefore, the number of new lousy women through these contacts transmitting the plague in the population is given by:
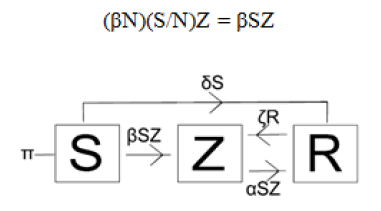
Basic model of contagion: We assume that a susceptible can avoid contagion by staying away from a louse by not having close contact, and each susceptible can resist the plague (in the case of boys having gel on their heads and girls having hair tied) at a rate of α. Thus, using the same idea as above with the probability Z/N of random contact of a susceptible with some lice (not the probability of a louse approaching a susceptible), the number of louses neutralized through this process per time unit per susceptible is:

The ordinary differential equation satisfies
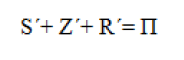
And therefore:
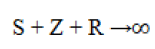
As t→∞, if Π≠0. Therefore S→∞, so this translates to a 'lice infestation' scenario: An outbreak of lice will lead to an infestation in the school environment, such as many children are already infected reaching adults.
If we assume that the outbreak occurs over a short time scale, then we can ignore looting rates. Therefore, we set out:
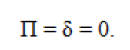
Setting the differential equations equal to 0 we have:
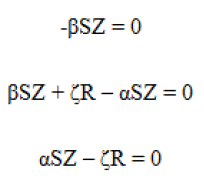
From the first equation, we have either S=0 or Z=0. So, this follows the form S=0 with this we get the piojistic equilibrium.
(S, Z, R)=(0, Z, 0)
When Z=0, we have the lice-free
equilibrium.(S, Z, R)=(N, 0, 0)
These equilibrium points show that, regardless of their stability, the child-employee coexistence is impossible.
The Jacobian is:
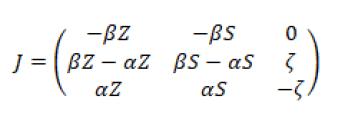
The lice free Jacobian is:
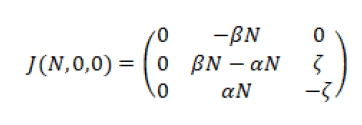
We have:
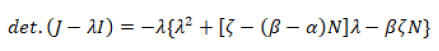
It follows that the characteristic equation always has a root with a positive real part. Therefore, the Lice-free equilibrium is always unstable.
Next, we have
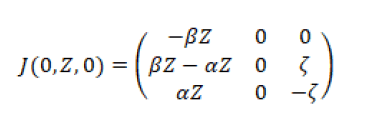
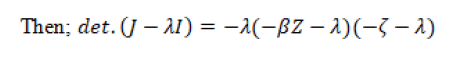
Since all the eigenvalues of the doomsday equilibrium are negative, it is asymptotically stable. It follows that, in a short outbreak, lice are likely to infect the entire population.
Spread of diseases with latent infection: We now revise the model to include a latent class of infected people, there is a period (approximately 33-35 days) after the child is a carrier of the louse, before they lice their classmates at school and others are carriers of the louse.
Thus, we extend the basic model to include the (more "realistic") possibility that a susceptible individual becomes infected before becoming libelous.
Changes to the basic model include:
• Susceptible first pass into a class of cloistered once infected and remain there for some period of time.
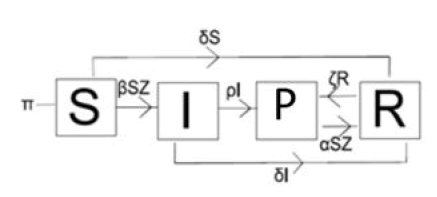
• The lice children can still be disinfected, if the plague is detected, and otherwise they become lice. We will refer to this as the SIZR model. The model is given by
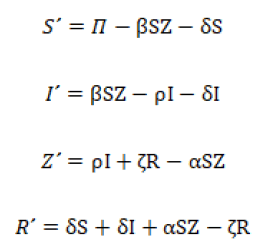
The SIZR model is illustrated
As before, if Π ≠ 0, then the infection overwhelms the child population. Consequently, we have again to assume a short time frame and hence Π=δ=0. Therefore, when we set the above equations to 0, we get either S=0 or Z=0 from the first equation. It follows once again from our analysis of the basic model that we achieve equilibrium:
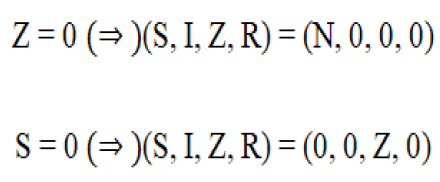
Therefore, the coexistence between healthy and empyema children again is not possible. In this case, the Jacobian we have:
First, we have:
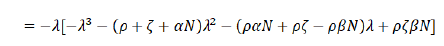
Where: ρζβN> 0, first we have: det (J(N,0,0,0)-λI) has an eigenvalue with a positive real part. Therefore, the lice-free equilibrium is unstable.
Next, we have:
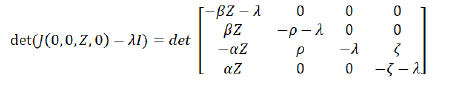
The eigenvalues are therefore λ=0, -βz, -ρ, . Since all eigen values are non-positive, it follows that the pest equilibrium is stable. Therefore, even with a latent period of infection, the lice will reproduce.
Dermatological treatment models: Suppose we can rapidly produce a cure for "grease lessness." Our treatment would be able to allow the lice-free individual to be lice free, however, the newly lice-infected would again be susceptible to becoming lice ridden; therefore, our cure does not provide immunity. Those lice who went through treatment and were allowed to enter the school, had their lice removed are children without lice before entering class R.
Things that need to be considered now include
• Since we have the treatment, we no longer need treatment.
• The cure will allow those who are meliorate not to be so regardless of how they acquired it.
• Any lice become susceptible again; the cure does not provide immunity.
Thus, the model with the treatment is given by
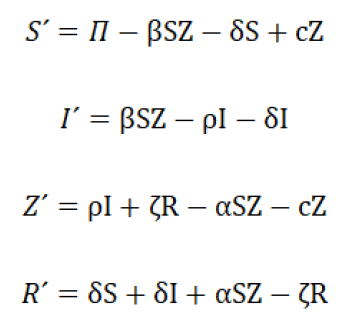
The model is illustrated
As in the other models, if Π ≠ 0, then S + I + Z →+ ∞R , so we can Π=δ=0, When z=0,
(S, I, Z, R)=(N, 0, 0, 0)
However, due to the cZ term in the first equation, we now have the possibility that an endemic equilibrium (S, I, Z, R) satisfies:
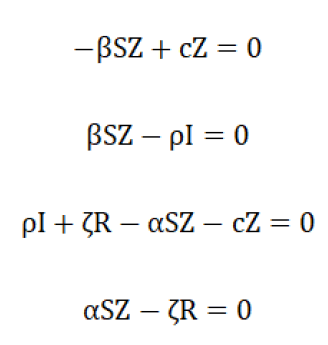
So the balance is:
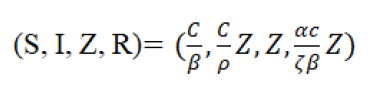
The Jacobian is:
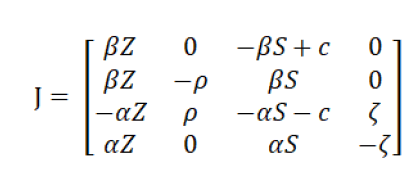
So, the balance does not remain:
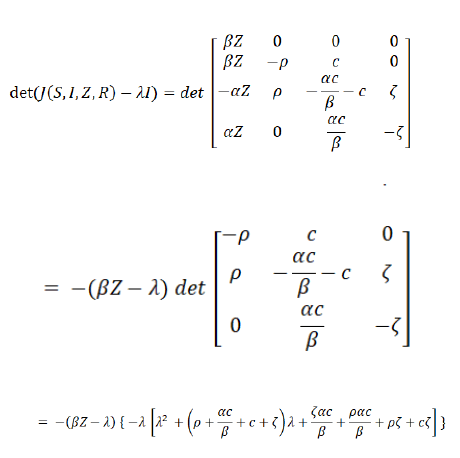
Since the quadratic expression has only positive coefficients, it follows that there are no positive eigenvalues. Therefore, the coexistence equilibrium is stable.
Impulsive eradication: Finally, an attempt was made to control the population of homeless people, obstructing the passage of infected children to school facilities or buildings, at those times that our policies allow. It was supposed to be difficult to have the resources and coordination, so he would have to check the kids more than once, and with each check, try to obstruct more lice. The result is an impulsive effect.
Here, we went back to the basic model and added the impulsive criteria:
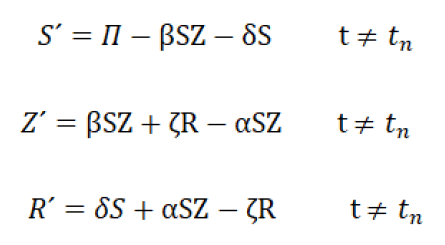
Contamination public health
In Mexico, the lice epidemic, year after year, has manifested itself in public and private schools, affecting above all the child population. Insects approximately one to two millimeters long that hides in clothing, bedding, and the scalp. This parasite causes inflammation, itching and sucks the blood of the person who hosts it (Figure 2).

Figure 2: Public health governance (diagraph).
Source: Elaborated with data study.
Lice are brown, oviparous insects that live exclusively on human hair and can be seen with the naked eye (they measure between two and three millimeters). They don't have wings and can't fly, but their six legs, which end in small claws, allow them to hold on tightly to fur. They also have a small head with mouth parts prepared to bite the scalp and suck the blood they feed on [9,10].
A louse lives between 33 and 35 days and goes through three stages:
Nit: For 6–7 days. It is the egg of the louse (an adult female lays and average of 110-150 during her life). It is attached to the base of the hair. Only 60% reach the adult louse. Nits differ from dandruff in that the former present great resistance when trying to be removed and cannot be removed with a simple wash.
Nymph: For 9–10 days. It is the louse just hatched from the egg. It is invisible to the human eye. Its body undergoes three growth molts until it becomes an adult and can reproduce.
Adult louse: For 15–16 days. The females deposit four to eight eggs daily at between one and two millimeters from the scalp.
Her favorite places: The hairs behind her ears, on the crown of her head, and on the back of her head. To ensure their adherence to the hair, they secrete a sticky and water insoluble substance that fixes the nit to the hair shaft.
According to information from the Mexican society of dermatology, in 2019 there is an epidemic in our country, which has manifested itself in public and private schools, and continues to affect the child population of our country. The louse does not discriminate against race or social status and despite the myths of most Mexicans, it is not a matter of poor hygiene, but rather they are spread by contact between people in closed places such as schools, workplaces, families, prisons and hospitals.
State of knowledge: Mathematical models of public health
Exponential function models: The exponential function is present in many growth phenomena: Animal, plant, economic, spread of epidemic diseases and others. In all of them the variable is time. It is also known as unlimited population growth. It serves to describe any process that evolves so that the increase (or decrease) in a small interval of time is proportional to what was at the beginning of it. That is, the rate of change of a population only depends on its size.
•It is reasonable for small populations in large environments.
•Population growth rate is proportional to its size. Graph of a function that satisfies the differential equation
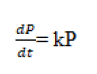
We must take into account the following considerations:
P=Population (dependent variable). t=Time (independent variable).
k=proportionality constant (parameter). Between the rate of population growth and its size.

Here we will treat only ordinary equation
Since it is proportional to the population, it is expressed as the product kP.
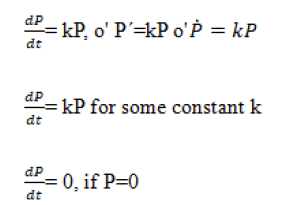
P (t) =0. This solution of a differential equation is called an equilibrium solution.
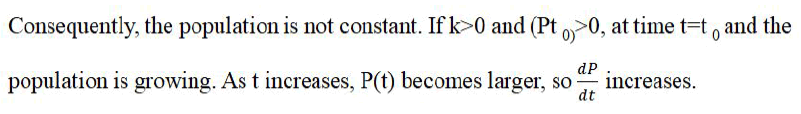
Logistic function model
The logistic function, logistic curve or S-shaped curve is a mathematical function that appears in various models of population growth, spread of epidemic diseases and spread in social networks. Said function constitutes a refinement of the exponential model for the growth of a magnitude. It was the Belgian mathematician, statistician, and astronomer Adolphe Quetelet who in 1835 proposed the idea that population growth was slowed down by a resistance proportional to the square of said population (mechanical hypothesis).
The logistic curve: To fit the exponential population growth model, you must take into account a limited environment and resources.
If the population is small, the rate of population growth is proportional to its size.
If the population is too large to be supported by its environment and resources, the population will decrease. That is, the growth ratio is negative.
Considerations:
t=time (independent variable).
P=Population (dependent variable).
k=growth rate coefficient for small populations (parameter).
We must consider that limited resources must enter another amount. This quantity is a second parameter, denoted by N (it will be called support capacity) of the environment.
In terms of carrying capacity, we assume that P(t) grows if P(t)<N; if P(t)>N is decreasing.
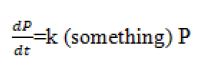
We add "something" close to 1, if P is small
But if we want "something" be negative
In this way, the logarithmic equation is as follows:
For this work we consider the following.
Where:
P(t): It is the population of prey (children) at the current time.
K: is the growth coefficient of the population of empiojadas.
P: Child population with lice.

What we see in the graph is that as there are outbreaks of lice, and children who are in close contact (given the characteristics of the children), the population of lice will increase continuously.
Lotka-Volterra model
Without a doubt, the mathematical function for calculating future populations that has aroused the most interest is the well-known ones: With the name of exponential, logistic and the Lotka-Volterra model and others. No species lives in isolation and interactions between species provide some of the most interesting models, here is a simple predator prey system of differential equations where one species "eats" the other, in this model we have two time dependent quantities. Our model then has two dependent variables that are both functions of time. In this case we will call the prey “school children” and the predators “lice”, and we will denote the prey S and the predators by P.
Lotka-Volterra growth model, also known as predator prey equations, are a pair of first order differential equations nonlinear that are used for modeling two interacting populations, a prey and a predator. The equations were independently proposed by Alfred J. Lotka in 1925 and Vito Volterra in 1926. Such equations are defined as:
This model is a bit more complicated than the basic SIR models that generally characterize infectious diseases as this model has two mass action transmissions, which leads to having more than one non-linear term in the model. Incidence specifies that an average member of the population makes enough contact to transmit the plague (βN) to others per unit of time or by too close contact, where N is the total population of children in the school (we assume that there is the closest contact). Nearby without lice. The probabilities that a random contact by a lousy person (Y/N), will turn another child lousy, therefore, the number of new lousy women through these contacts transmitting the plague in the population is given by:

Basic model of contagion: We assume that a susceptible can avoid contagion by staying away from a louse by not having close contact, and each susceptible can resist the plague (in the case of boys having gel on their heads and girls having hair tied) at a rate of α. Thus, using the same idea as above with the probability Z/N of random contact of a susceptible with some lice (not the probability of a louse approaching a susceptible), the number of louses neutralized through this process per time unit per susceptible is:

The ordinary differential equation satisfies
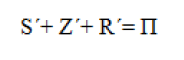
And therefore:
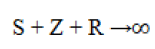
As t→∞, if Π≠0. Therefore S→∞, so this translates to a 'lice infestation' scenario: An outbreak of lice will lead to an infestation in the school environment, such as many children are already infected reaching adults.
If we assume that the outbreak occurs over a short time scale, then we can ignore looting rates. Therefore, we set out:
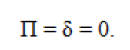
Setting the differential equations equal to 0 we have:
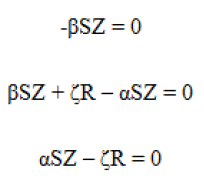
From the first equation, we have either S=0 or Z=0. So, this follows the form S=0 with this we get the piojistic equilibrium.
(S, Z, R)=(0, Z, 0)
When Z=0, we have the lice-free
equilibrium.(S, Z, R)=(N, 0, 0)
These equilibrium points show that, regardless of their stability, the child-employee coexistence is impossible.
The Jacobian is:
The lice free Jacobian is:
We have:
It follows that the characteristic equation always has a root with a positive real part. Therefore, the Lice-free equilibrium is always unstable.
Next, we have
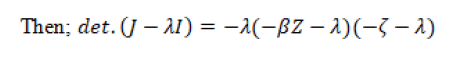
Since all the eigenvalues of the doomsday equilibrium are negative, it is asymptotically stable. It follows that, in a short outbreak, lice are likely to infect the entire population.
Spread of diseases with latent infection: We now revise the model to include a latent class of infected people, there is a period (approximately 33-35 days) after the child is a carrier of the louse, before they lice their classmates at school and others are carriers of the louse.
Thus, we extend the basic model to include the (more "realistic") possibility that a susceptible individual becomes infected before becoming libelous.
Changes to the basic model include:
• Susceptible first pass into a class of cloistered once infected and remain there for some period of time.
• The lice children can still be disinfected, if the plague is detected, and otherwise they become lice. We will refer to this as the SIZR model. The model is given by
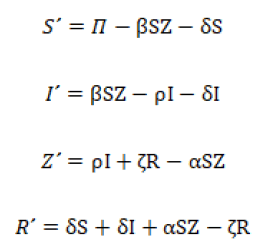
The SIZR model is illustrated

As before, if Π ≠ 0, then the infection overwhelms the child population. Consequently, we have again to assume a short time frame and hence Π=δ=0. Therefore, when we set the above equations to 0, we get either S=0 or Z=0 from the first equation. It follows once again from our analysis of the basic model that we achieve equilibrium:
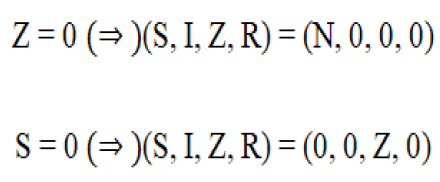
Therefore, the coexistence between healthy and empyema children again is not possible. In this case, the Jacobian we have:
First, we have:
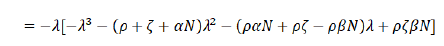
Where: ρζβN> 0, first we have: det (J(N,0,0,0)-λI) has an eigenvalue with a positive real part. Therefore, the lice-free equilibrium is unstable.
Next, we have:
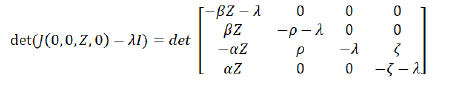
The eigenvalues are therefore λ=0, -βz, -ρ, . Since all eigen values are non-positive, it follows that the pest equilibrium is stable. Therefore, even with a latent period of infection, the lice will reproduce.
Dermatological treatment models: Suppose we can rapidly produce a cure for "grease lessness." Our treatment would be able to allow the lice-free individual to be lice free, however, the newly lice-infected would again be susceptible to becoming lice ridden; therefore, our cure does not provide immunity. Those lice who went through treatment and were allowed to enter the school, had their lice removed are children without lice before entering class R.
Things that need to be considered now include
• Since we have the treatment, we no longer need treatment.
• The cure will allow those who are meliorate not to be so regardless of how they acquired it.
• Any lice become susceptible again; the cure does not provide immunity.
Thus, the model with the treatment is given by
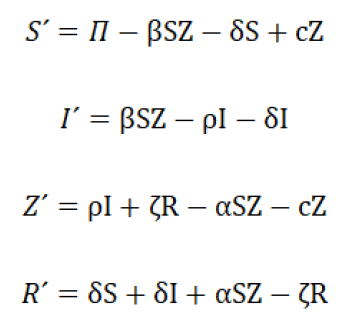
The model is illustrated

As in the other models, if Π ≠ 0, then S + I + Z →+ ∞R , so we can Π=δ=0, When z=0,
(S, I, Z, R)=(N, 0, 0, 0)
However, due to the cZ term in the first equation, we now have the possibility that an endemic equilibrium (S, I, Z, R) satisfies:
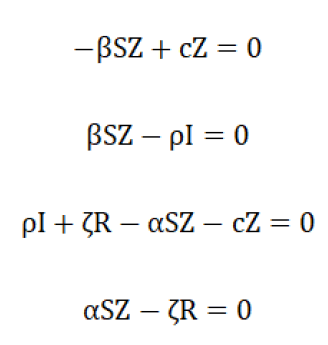
So the balance is:
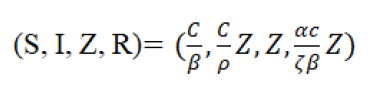
The Jacobian is:
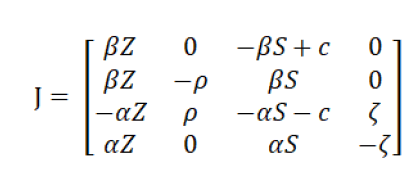
So, the balance does not remain:
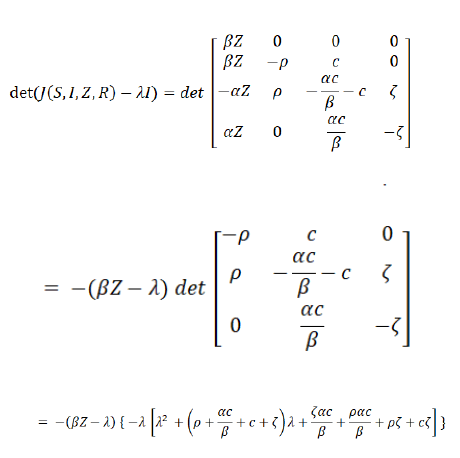
Since the quadratic expression has only positive coefficients, it follows that there are no positive eigenvalues. Therefore, the coexistence equilibrium is stable.
Impulsive eradication: Finally, an attempt was made to control the population of homeless people, obstructing the passage of infected children to school facilities or buildings, at those times that our policies allow. It was supposed to be difficult to have the resources and coordination, so he would have to check the kids more than once, and with each check, try to obstruct more lice. The result is an impulsive effect.
Here, we went back to the basic model and added the impulsive criteria:
The contribution of this work to the state of knowledge lies in the formalization of mathematical models for the study of the governance of dermatological health in vulnerable groups. This is a discussion about the scope and limits of the models to demonstrate their usefulness in decision making, the establishment of prevention programs and the dissemination of self-care styles. Public health governance can be built from the conflict between the parties involved. Public and private, social and political actors can activate a negotiation, reach consensus and establish co responsibilities if the forecasts of the models are considered. In the case of the exponential growth model that poses a collateral pandemic to COVID-19, the present work established that it is the most likely approximation. In a double epidemic scenario, the rulers and the ruled can reach an agreement if public health governance is prioritized. Educational systems under a prevention and self-care policy represent a feasible scenario. The parties involved can achieve co responsibility from the negotiation of returning to the virtual classroom. Social work has the instruments to implement public health governance to demonstrate that the virtual educational system is as effective as the traditional face to face classroom. The prevention of both pandemics, that of the coronavirus and that of COVID-19, can be established from confinement and distancing of people with the assistance of social work.
Citation: Guillen JC. "Public Health Governance in the COVID-19 Era ". Health Econ Outcome Res, 2022, 8(12), 1-7.
Received: 05-Aug-2022, Manuscript No. HEOR-22-71319; Editor assigned: 08-Aug-2022, Pre QC No. HEOR-22-71319 (PQ); Reviewed: 22-Aug-2022, QC No. HEOR-22-71319; Revised: 21-Dec-2022, Manuscript No. HEOR-22-71319 (R); Published: 30-Dec-2022, DOI: 10.37532/2471-268X.10.1.005
Copyright: © 2022 Guillen JC. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.