Short Communication - (2017) Volume 3, Issue 2
The success of cooperative ventures is often highly dependent on the rules that govern participants. This is especially true when the stakes are high, as is so often the case when medical devices/facilities are shared and costs are large in terms of both dollars and patient congestion/delay. We argue that one cost sharing mechanism, namely the serial cost sharing rule, enjoys extraordinary equity and incentive properties and is especially well suited for adoption in health care contexts. Moreover, serial cost sharing is the one and only cost sharing rule to be endowed with these powerful equity and incentive features.
Keywords: Medical; Health care; MRI scanner; Surgical facility; Overexploit; Defections; Mechanism; Quality; Stochastic shocks
The skyrocketing costs associated with contemporary high tech medical devices and surgical facilities have increasingly incentivized the joint use of such facilities by multiple users. The success of such cooperative arrangements can, however, be highly sensitive to the manner in which resultant costs are shared. Cost sharing systems that are ill-suited to their application can lead to a host of serious problems ranging from open hostility between users as a consequence of perceived injustice to sub-optimal facility use as a consequence of improper incentives. Such concerns are by no means unique to the health care industry and are in fact endemic to everything from complex computer networks to the simple sharing of a lawnmower between two neighbors. For in depth presentations on cost and resource allocation problems we can refer Moulin [1] and Hougaard [2]. The extraordinarily high stakes present in health care contexts will, however, tend to amplify the detrimental consequences of adopting an ill-advised cost sharing procedure. In particular, one “cost” to be shared in many health care contexts is that of patient delay. The fact that patients sometimes, rightly or wrongly, perceive the delay of their service as a matter of life and death can lead to delay costs being of paramount concern in the maintenance of successful medical practices.
The purpose of this paper is to provide a brief and nontechnical overviews of cost sharing in environments where costs are convex, i.e., are increasing at a non-decreasing rate. We provide a discussion of cost sharing rules that are commonly employed in practice and single out one cost sharing procedure, the serial cost sharing rule, as particularly well suited for many health care contexts. We argue that serial cost sharing is endowed with compelling equity properties, extraordinary incentive properties, and is the only cost sharing procedure to enjoy these properties.
We will use the phrase “cost sharing game” to refer to environments in which a finite number of agents (e.g., individual physicians or consortiums of physicians that operate collectively as units) place demands on a productive facility (e.g., an MRI scanner or surgical facility) and in return for this shared access, are obligated to share requisite costs in accordance with a pre-specified rule. The costs to be shared are themselves assumed to be convex in the aggregate demands placed on the facility. These costs can involve traditional production costs such as staffing, equipment, and maintenance costs, but can also involve patient delay costs. Although a detailed discussion of uncertainty is beyond the scope of this paper, it should be further noted that the results discussed below can be extended to contexts in which costs, benefits, and quality of service can all be impacted by stochastic “shocks” such as random breakdowns or medical procedures that encounter unexpected complications. See Kolpin and Wilbur [3] for a detailed, formal analysis of such Bayesian cost share games.
Readers may recall Adam Smith’s [4] notion of an “invisible hand” that guides markets so that the self-interested decisions of individuals will lead to socially desirable outcomes. One critical observation in the shared facility context is that the implementation of a cost sharing rule effectively shapes the “local market” of a shared facility in ways that are not necessarily favorable to the society being served. Indeed, many of the rules most frequently considered for adoption are prone to eliciting ill-behavior on the part of participants. We will show that that there is one and only one rule that does not suffer from this defect, namely, the serial cost share rule. As such, one may view the well-thought out selection of a cost sharing rule as a means for providing the invisible hand with some benevolent assistance.
Let us now turn to an overview of cost sharing rules commonly observed in practice.
Per capita cost sharing: One natural and transparently equitable (with respect to equal treatment across agents) method of sharing costs is to dictate that all costs are shared equally across the set of agents. This may superficially appear to be a perfectly sensible and fair way of allocating costs when participating agents are sufficiently similar (e.g., physicians with patient pools of comparable size and composition). However, if agents have discretionary control over the size of their demands, then implementation of per capita cost sharing can induce a veritable tragedy of the commons [5] wherein users effectively overexploit a common pool resource. To see this, simply note that when a given agent contemplates the consequences of increasing the demands that it places on the shared facility, the agent is aware that it will pay but a fraction of the corresponding incremental cost. Indeed, if there are n agents sharing the facility, then the given agent will only be required to pay 1/n of the corresponding incremental cost. Agents are thus induced to overexploit the shared facility and in the resulting equilibrium, all agents would fare better if they were each to reduce their demands.
Average cost sharing: Another natural and transparently equitable (with respect to equal treatment across units of demand) cost sharing procedure is that in which total costs are distributed equally across each unit of demand. In this procedure, the total cost of satisfying the sum of each agent’s demands is calculated. This total cost is then divided by the aggregate demand itself so as to derive a common unit “sharing price.” By construction, this price is precisely that which will lead all costs to be covered when each agent’s cost share is equated to the product of this unit price and the agent’s total facility demand. When the cost function is strictly convex, a tragedy of the commons can once again emerge as agents realize that they will only be required to pay a fraction of the incremental costs that their demands impose on the group as a whole. Over-exploitation can thus emerge in equilibrium and agents can collectively improve their situation by coordinating a reduction in their demands.
There is, of course, a multitude of cost sharing rules one could hypothetically implement. We will argue that one, the serial cost share rule, uniquely stands out as enjoying superior equity and incentive properties. As a preliminary motivation for the structure of this rule, consider the following example.
Dr. Small and Dr. Large share a facility capable of producing up to 100 units of output at a marginal cost of one dollar per unit, but if forced to produce beyond this level, additional output can only be produced at a marginal cost of nine dollars per unit. Suppose further that Small demands 20 units and large demands 180 units, resulting in an average production cost of 5=(100+100×9)/200 dollars per unit. If costs are covered through the imposition of a $5 price per unit demanded, it follows that Small’s total bill is $100 while Large’s is $900. Small may, however, feel cheated in such an arrangement as Small knows that if Large had shared demands even roughly on par with those of Small, the aggregate demands placed on the facility would have been well under 100 and average production costs would have been only one dollar rather than five. If forced to pay $100, Small would effectively be subsidizing Large’s exorbitant demands. Consequently, Small may feel fully justified in arguing that Small should not be compelled to pay one penny more than $20.
This example points the way to a resolution of Small’s claims of injustice. In particular, let us suppose that both Small and Large were to pay the same amount for the first 20 units of their demand and that this payment was set equal to $20 each–an amount that is just sufficient to cover the costs of a 40 unit aggregate demand that includes Small’s 20 unit total and the first 20 units of Large’s demand. Large, however, has an incremental demand of 160 units beyond Large’s initial 20 units of demand. As such, it can be argued that Large should be obligated to pay the full incremental cost of this incremental demand. In particular, in addition to the $20 payment for the first 20 units demanded, Large should pay an additional $960=60×1+100×9 for its final 160 units of demand.
The cost shares outlined above describe serial cost sharing in the context of this simple example. Loosely speaking, the serial cost sharing rule can be described as the procedure that (1) evenly distributes the production costs that result when each agent’s demands are hypothetically constrained by those of the smallest user and (2) allocates residual costs to residual agents (those with greater demands) through recursive application of this procedure. In effect, each user’s cost share is independent of any incremental demands that are above and beyond their own. For those interested in a more detailed formulation of serial cost sharing, it can be articulated as follows.
Definition-serial cost sharing: Order all user demands from smallest to largest, labelling demands as x1 through xn and let x0=0. For each i=1,…,n, assign to all users whose demands are at or above xi an equal share of the incremental cost generated by the xi -xi-1 units of each agent’s demand that are above and beyond their first xi-1 units of demand. Formally, this incremental cost share is equal to:
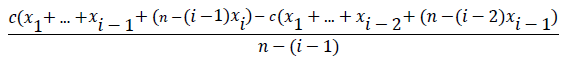
Each user’s comprehensive cost share is then the sum of all incremental cost shares that have been assigned to that user.
Although our simple fable of a facility shared by doctors Large and Small may paint a compelling story for serial cost sharing in that narrow context, this does not in of itself imply that it is a reasonable cost allocation mechanism to adopt in more general settings. We next show that serial cost sharing does in fact prove to be endowed with powerful equity and incentive properties.
Excess demand protection: Detailed axiomatic analyses of the serial cost sharing rule have been presented in such papers as Moulin and Shenker [6] and Kolpin [7]. These papers establish axiomatic characterizations of “fair” cost sharing and demonstrate that these characterizations lead only to serial cost sharing. Aadland and Kolpin [8,9] take a concrete practical perspective and examine serial cost sharing in the context of shared irrigation costs. Through a series of interviews and surveys of actual participants in these cooperative ventures it is found that a defining feature of serial cost sharing, both theoretically and from the perspectives of the users themselves, is the excess demand protection principle. This principle asserts that each agent should be protected from the excessive demands of others, a compelling principle whenever costs are convex, as is often the case in health care contexts.
The equity attributes of cost sharing procedures should not be taken lightly. Indeed, human experience has repeatedly proven that perceived injustice can be a significant force in tearing asunder what had once been fruitful collaborations. Examples can be found in everything from large scale international conflicts to the dissolution of a marriage. With that said, the strategic incentives embodied by serial cost sharing are also extraordinarily important. An objectively “fair” sharing rule is unlikely to be considered of much value if it encourages widespread “abuse” of the shared facility in question. The serial cost sharing rule is, however, uniquely endowed with important incentive properties. An incomplete list is briefly outlined below.
Coalitional stability: As readers may recall, Nash equilibrium is a profile of strategies for which no individual player has an incentive to modify its strategy given the strategies of others. In the context of cost sharing, a Nash equilibrium is profile of facility utilization plans for each agent such that no agent has an incentive to alter its plans given the plans of others. While Nash equilibrium are innately robust to unilateral “defections” of any individual agent, this is not generally true of coalitions. Consider the well-known prisoner’s dilemma where two criminals are interrogated regarding their joint complicity in a crime. The unique equilibrium of this game is for each individual to confess to their crime in a quest for preferred treatment. However, this equilibrium also has the property that if both individuals were to have remain tight-lipped about their exploits they would each have been strictly better off. That is, if these two individuals had been able to form a coalition and coordinate their statements in the interrogation room they would have been able to improve their situation. The serial cost-sharing rule is immune to such incentives for coalitional defection. In fact, any efforts from a coalition of agents to “defect” from equilibrium will necessarily lead to at least one coalition member to become strictly worse off, thereby neutralizing any coalition defection incentives. This is a defining feature of the serial cost sharing rule, that is, it is the one and only cost sharing rule to enjoy this property of coalitional stability [10].
Transparent system solutions: Generally speaking, cost sharing games can have multiple equilibrium, making it difficult to predict the precise usage patterns to be expected of participants. Moreover, even if the number of these equilibrium is limited, they can nonetheless be exceedingly difficult calculate, drawing into question how long it will take such environments to exhibit equilibrium behavior. Such concerns do not apply when serial cost sharing governs facility access. Indeed, the implementation of serial cost sharing induces a unique equilibrium in the resulting environment. Moreover, this unique equilibrium can quickly and easily be calculated by applying a straightforward process of recursively eliminating strictly “dominated” strategies [3]. The serial cost sharing rule is the only mechanism to exhibit this feature.
The prospects for the successful sharing of productive facilities among multiple users can often be undermined by behavior induced by the rules that govern facility access. Persistent perceptions of injustice can simmer and some participants may ultimately seek out alternative partnerships should they perceive governance rules as being “rigged” against them. Some of the most commonly used cost sharing methods are also prone to inducing environments that encourage over-exploitation of the shared facility. The consequences of such tendencies are especially severe in health care contexts where both the dollar costs and the patient delay costs are high. This paper draws attention to these concerns as well as presents a solution in the form of the serial cost sharing rule. This mechanism protects users from the costs generated by the excessive demands of others, it is invulnerable to coalition defections, and the equilibrium consequences of implementing the process are both predictable and easy to calculate. Moreover, serial cost sharing is the only cost sharing mechanism to enjoy these features and this result persists even in the presence of stochastic shocks to costs, benefits, and quality of service.