Research - (2019) Volume 11, Issue 6
Background: Dengue is one of the most serious and fast emerging tropical diseases. In India, over the past decade, Dengue fever has increased in frequency and geographical extent. Detailed information about when and where DF/DHF outbreaks occurred in the past can be used for epidemiological modeling to predict future trends and impending outbreaks. Based on this background, an attempt was made to convert the available monthly data of dengue fever incidence in the Kerala state into seasonal ARIMA model to forecast disease burden.
Methods: The current study was retrospective analytical study using secondary data from department of Director of Public Health of Kerala state, India. The monthly reports of integrated disease surveillance project (IDSP) for a period of thirteen years from 2006 to 2018 were downloaded and data of dengue fever cases was extracted from the downloaded pdf files. Using SPSS trial version 21 and a sample data set, several ARIMA models were run and best suited seasonal ARIMA model was identified. The selected model was then used to forecast monthly dengue fever incidence from the next coming year i.e. from 2007 onwards. Monthly forecasted incidence and monthly real incidence of dengue fever cases from 2007 to 2018 were compared and the difference between them was tested using paired t test.
Results: Seasonal ARIMA (1, 0, 0) (0, 1, 1)12 model was found to be the best fitted model for the given data. Stationary R square value of selected models is 0.815. Ljung–Box test value is 11.271 and p value is 0.792, indicating that the selected model is adequate. Average number of forecasted incidence of dengue fever cases from January 2007 to December 2018 were nearer to the real incidence in every month, but the difference among them was not statistically significant, indicating that the model fit was good.
Conclusion: A Seasonal ARIMA (1, 0, 0) (0, 1, 1)12 was selected as best suited model to predict the future incidence of dengue fever cases in the forthcoming period. The technique would be useful for health care administrators for better preparedness. The model can be made dynamic to include the current data and for a more dynamic model.
ARIMA model; Dengue fever; Predictive analysis; Time series analysis
Dengue is one of the most serious and fast emerging tropical diseases. Its burden in certain socio-ecological settings can be paralleled with that of malaria. It is causing 4,65,000 DALYs across the globe [1]. Dengue infection in humans results from four dengue virus serotypes (DEN-1, DEN-2, DEN-3, and DEN-4) of Flavivirus genus which are singlestranded positive polarity ribonucleic acid (RNA) viruses. Aedes aegypti is the principal vector transmitting Dengue virus (DENV) from person to person. It is also transmitted by Aedes albopictus [1–3]. Dengue, with its two severe clinical manifestations – dengue haemorrhagic fever (DHF) and dengue shock syndrome (DSS), poses an increasingly perilous situation due to lack of specific antiviral drugs or vaccine [4]. The global incidence of dengue fever (DF) and dengue hemorrhagic fever (DHF) has increased in recent decades [5]. Today about 2.5 billion people, or 40% of the world’s population, live in areas where there is a risk of dengue transmission. The World Health Organization (WHO) estimates that 50 to 100 million infections occurs yearly, including 500,000 DHF cases and 22,000 deaths, mostly among children [6]
In India, over the past decade, Dengue fever increased in frequency and in geographical extent [7]. Now every state in India is reporting dengue fever cases every year. Among them Kerala is one of the high risk states reporting more number of cases every year [7]. Since 2007, diagnosis and data assimilation for dengue and chikungunya in India have been facilitated by the National Vector Borne Disease Control Programme (NVBDCP) [3]. Dengue fever had a predominant urban distribution a few decades earlier, but is now also reported from peri-urban as well as rural areas. Surveillance for dengue fever in India is conducted through a network of more than 600 sentinel hospitals under the NVBDCP program [8]. Every day, integrated disease surveillance program is providing district wise data of dengue fever cases in Kerala state. IDSP providing annual reports containing monthly incidence of dengue fever cases in each district [9]. However only the number of cases are available, and they are not presented as epidemiological parameters such as epidemic curves or incidence rates.
The epidemiologic parameters are useful to monitor the trend and fluctuations of dengue fever to identify related epidemiological factors and effectiveness of control measures. Detailed information about when and where DF/DHF outbreaks occurred in the past can be used for epidemiological modeling to predict future trends and outbreaks. This enables the health systems for better preparedness to plan and allocate resources for effective control of future outbreaks. Auto Regressive Integrated Moving Averages (ARIMA) modeling using time series analysis has been increasingly used in the field of epidemiological research on infectious diseases, such as influenza, malaria and dengue. Wang C conducted a study on morbidity profile of influenza in China using ARIMA analysis [10]. Anwar forecasted future trends of malaria incidence in Afghanistan using time series analysis [11]. Siregar and Lal also used ARIMA analysis to forecast dengue fever incidence in India in their studies [12,13]. Ho CC, Ting C-Y presented a paper on the time-series modelling of accumulated dengue fever cases acquired from the Malaysian Open Data Government Portal [14].
Statistical forecasting methods such as ARIMA are based on the assumption that the time series can be rendered approximately stationary. A stationary time series is one whose statistical properties such as mean and variance are constant over time. Autoregressive integrated moving average (ARIMA) models, have been used for statistical modeling and analyzing time series data to develop a predictive forecasting model [10]. ARIMA model has three components “AR (Auto Regression)”, “I (Integration)” and “MA (Moving Average)”. The “AR” part indicates that the forecasted variable of interest is regressed on prior values. The “I” part indicates that the data values have been replaced with the difference between their values and the previous values. The “MA” part indicates that the regression error is actually a linear combination of error terms whose values occurred contemporaneously and at various times in the past. The purpose of each of these features is to make the model fit the data as well as possible. There are two types of ARIMA models Non-seasonal ARIMA model and seasonal ARIMA model. Non-seasonal ARIMA models are generally denoted ARIMA (p, d, q) where parameters p, d, and q are non-negative integers, p is the order (number of time lags) of the autoregressive model. It allows incorporating the effect of past values into the model. This would be similar to stating that if it is likely to be warm tomorrow if it has been warm for the past three days. d is the degree of differencing (the number of times the data have had past values subtracted) to make the model stationary i.e. avoiding a rising or falling trend. It is like stating that the temperature tomorrow would be the same if the difference in temperature over the past three days has been small. q is the order or size of the of the moving-average model in the average temperature for a given day can be calculated based on preceding and succeeding 1, 3, 5, 7 days. Seasonal ARIMA models are usually denoted ARIMA (p, d, q) (P, D, Q)m, where m refers to the number of periods in each season, and the uppercase P, D, Q refer to the autoregressive, differencing, and moving average terms for the seasonal part of the ARIMA model. Seasonal ARIMA model can be used if the data of more than one year is available, and Non-seasonal ARIMA model can be used if the data of only few months is available [15,16].
Based on this background, an attempt was made to convert the available monthly data of dengue fever incidence in the Kerala state into useful seasonal ARIMA model. The aim of current study was to develop a suitable seasonal ARIMA model which can be used to forecast the future incidence of dengue in the forthcoming month or period or year for a given geographical location, Kerala state in this instance.
The current study was retrospective analytical study using secondary data from Kerala state. Study was conducted during the period from April 2019 to June 2019. People living in the Kerala state were considered as study population. Data of Kerala people suffered with dengue fever from the year 2006 to 2018 was used for the study. Study was conducted using the secondary data and there is no direct involvement of the study participants.
Department of Director of Public Health of Kerala state (http://dhs.kerala.gov.in/index.php/ publichealth) is providing annual reports of month wise incidence of communicable disease in Kerala state [9]. The annual reports for a period of thirteen years from 2006 to 2018 were downloaded and data of dengue fever cases was extracted from the downloaded pdf files. Suspected dengue cases in all the districts of Kerala were included in the study. No case was excluded from the annual reports. Average monthly incidence rates were calculated using MS Excel software for the period 2006 to 2018 and observed the trend of dengue fever incidence. Using SPSS trial version 21 and a sample data set, several ARIMA models were run and best suited seasonal ARIMA model was identified. The selected model was then used to forecast monthly dengue fever incidence from the next coming year i.e. from 2007 onwards. Monthly forecasted incidence and monthly real incidence of dengue fever cases from 2007 to 2018 were compared and the difference between them was tested using paired t test.
Statistical analysis
Expert Modeller in SPSS trial version 21 automatically identifies and estimates the bestfitting ARIMA or exponential smoothing model for one or more dependent variable series, thus eliminating the need to identify an appropriate model through trial and error. The order of p, d, q values and P, D, Q values for auto regression (AR), integration (I) and moving average (MA) will be automatically detected using “Expert Modeller” option [17,18]. For model creation, month wise incidence of dengue fever cases from the year 2006 to 2018 was selected as a dependent variable and “Expert Modeller” as the method. The Predictive values, Lower confidence limits, Upper confidence limits, were saved.
The model with the best fit was selected for forecasting. It was tested for adequacy using the Ljung–Box test. A significant value less than 0.05 were considered to acknowledge the presence of structure in the observed series, which was not accounted for by the model; therefore, we ignored the model if it had significant value. A model with p value more than 0.05 was considered as adequate model, as the observed values are discrete, independent and identically distributed which is considered as white noise pattern [15]. The best selected model was used to forecast monthly dengue fever incidence for the next coming year i.e. from 2007 onwards. Monthly forecasted incidence and monthly real incidence of dengue fever cases from 2007 to 2018 were compared. The difference between forecasted and real incidence was tested using paired t test.
Figure 1 depicts the average monthly incidence of dengue fever cases in Kerala state since the year 2006. It can be observed that the average monthly incidence of dengue fever cases gradually rose from the year 2006 to 2018. Sudden decline of incidence can be observed in the year 2011, 2014 and 2018.There is a sudden rise of incidence in the year 2017.
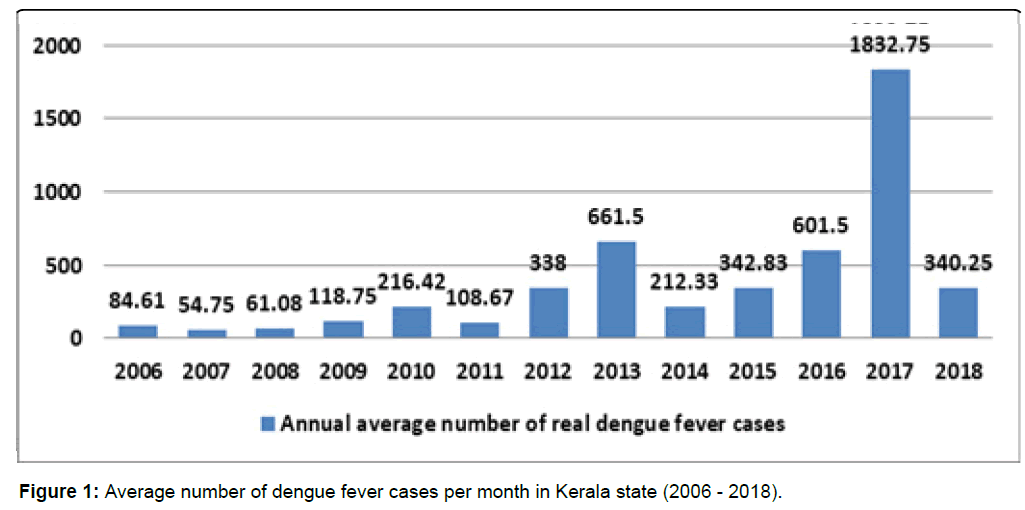
Figure 1. Average number of dengue fever cases per month in Kerala state (2006 - 2018).
“Expert modeller” of SPSS identified the current periodicity as 12 in the selected data. Seasonal ARIMA (1, 0, 0) (0, 1, 1)12 model was identified as best fitted model for the given data. It gave the predictive values 12 months after the starting of selected period, i.e. from January 2007 to December 2018. Difference between real value and the predictive value in each month will be called as residual of the model. Autocorrelation factor (ACF) and partial autocorrelation factor (PACF) was tested for residuals to observe the pattern of residuals. Residuals should not show any significant pattern, then only the selected model will be considered as best fitted model. Figure 2 depicts the auto correlation and partial auto correlation of predicted cases at different lag times. Two lines in the graph indicate the 95% confidence limits of Residual ACF and Residual PACF. At any lag time Residual ACF and Residual PACF not crossed the 95% confidence limits. It revealed that there were no significant ACF and PACF between residuals at different lag times. It showed that, residuals not showing any significant pattern and they were discrete, independent and identically distributed i.e. showing white noise pattern. Table 1 depicts the model fit statistics and Ljung–Box test for residuals of selected predictive model i.e. seasonal ARIMA (1, 0, 0) (0, 1, 1)12. Stationary R square value of selected models is 0.815. Ljung–Box test value is 11.271 and p value is 0.792 which is not significant.
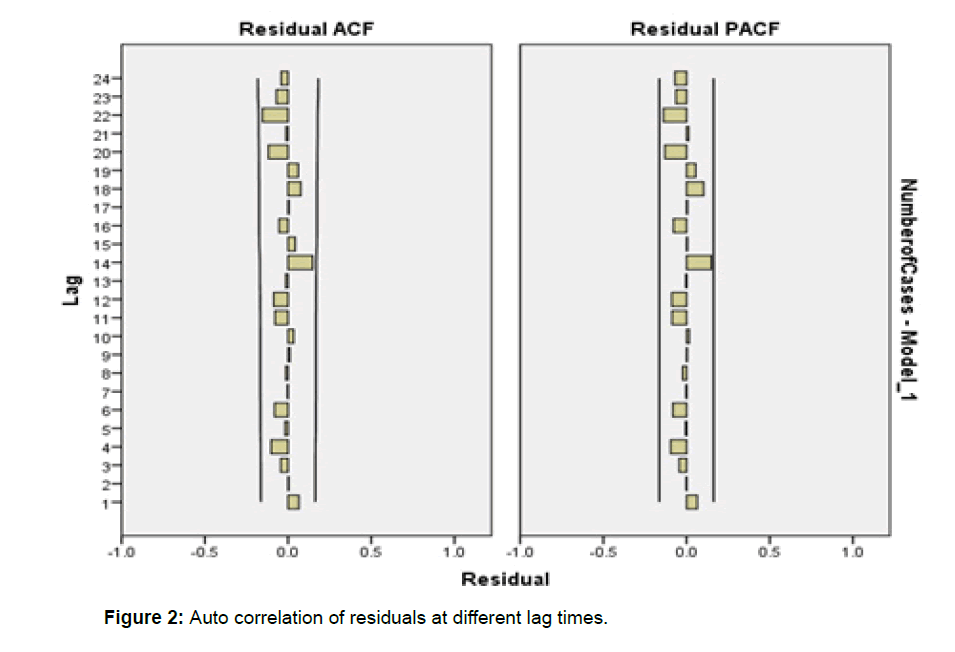
Figure 2. Auto correlation of residuals at different lag times.
| Model | Model Fit statistics | Ljung-Box Q(18) | ||
|---|---|---|---|---|
| Stationary R-squared | Statistics | DF | Sig. |
|
| Seasonal ARIMA (1, 0, 0) (0, 1, 1)12 | .815 | 11.271 | 16 | .792 |
Table 1: Model Ljung-Box statistics of ARIMA (1, 0, 0) (0, 1, 1)12.
Based on the above the seasonal ARIMA (1, 0, 0) (0, 1, 1)12 was used to forecast the monthly dengue fever incidence for each month from the January 2007 to December 2018. Figure 3 shows the forecasted monthly incidence and real incidence of dengue fever cases from January 2007 to December 2018. The graph shows that the predicted model fits well with the actual data.
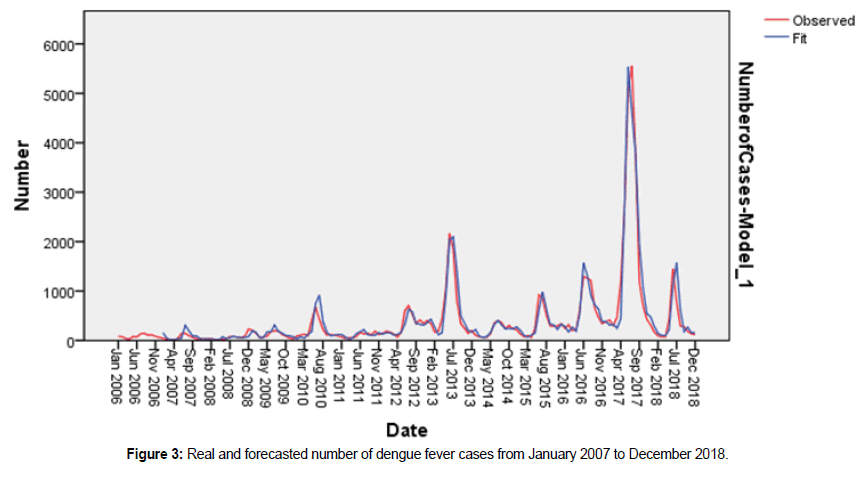
Figure 3. Real and forecasted number of dengue fever cases from January 2007 to December 2018.
To further test the adequacy of fit the annual average number of forecasted incidence and real incidence of dengue fever cases from 2007 to 2018 were compared using paired t test. Table 2 depicts the average number of forecasted and real incidence of dengue fever cases per month from 2007 to 2018. The differences in the values year to year were not statistically significant indicating that the model fits well.
| Year | N | Average number of predicted dengue fever cases per month | Average number of real dengue fever cases per month | t statistic | p value |
|---|---|---|---|---|---|
| 2007 | 12 | 86.79 | 54.75 | -1.652 | 0.127 |
| 2008 | 12 | 49.27 | 61.08 | 0.846 | 0.416 |
| 2009 | 12 | 143.85 | 118.75 | -2.031 | 0.67 |
| 2010 | 12 | 249.27 | 216.42 | -0.671 | 0.516 |
| 2011 | 12 | 117.38 | 108.67 | -0.641 | 0.535 |
| 2012 | 12 | 298 | 338 | 1.591 | 0.140 |
| 2013 | 12 | 719.88 | 661.5 | -0.881 | 0.397 |
| 2014 | 12 | 218.84 | 212.33 | -0.479 | 0.642 |
| 2015 | 12 | 339.37 | 342.83 | 0.100 | 0.922 |
| 2016 | 12 | 614.07 | 601.50 | -0.292 | 0.776 |
| 2017 | 12 | 1830.32 | 1832.75 | 0.018 | 0.986 |
| 2018 | 12 | 408.71 | 340.25 | -0.825 | 0.427 |
Table 2: Comparison of forecasted and real incidence of dengue fever cases from the year 2007 to 2018.
Since the 1990s, epidemics of dengue have become more frequent in many parts of India. During the period from 2010–2014, 213607 cases (incidence: 34.81 per million population) of dengue fever were observed and the number of dengue cases during this period has increased markedly, by a factor of ~2.6, with respect to the 1998–2009 period. High dengue incidence, ranging between 21 and 50 per million, was reported for the states of Punjab, Gujarat, Karnataka, Kerala, Tamil Nadu and Orissa [19]. The daily incidence of dengue fever and other communicable diseases was monitored by the integrated disease surveillance program (IDSP).
Surveillance data of the communicable diseases is very useful to the administrators for monitoring trends of incidence daily. But the usefulness of that data can be extended with the help of statistical analysis. It can be used to know the loopholes in the reporting system, to know the peak period of incidence of disease in a season. Apart from these benefits, predictive analysis gives us a scope to predict the future burden of disease also i.e. to predict an epidemic early [13,14,20,21].
Predictive ARIMA models were used by many researchers to forecast the burden of dengue fever cases. Most of the researchers used the data of several years for their analysis and used Seasonal ARIMA model for forecasting. Same procedure was used in the current study. A thirteen years monthly incidence data of dengue fever cases in the Kerala state from the year 2006 to 2018 was used in the current study. Seasonal ARIMA (1, 0, 0) (0, 1, 1)12 was selected as best suited model to predict the future incidence of dengue fever cases in the forthcoming period of days, weeks, months or year. This model is useful to health care administrators to predict what would happen in the next period. Predictions of shorter time duration are feasible if the relevant data is made available.
Lal et al., in their study conducted at Rajasthan, India, stated that Seasonal ARIMA (0, 0, 1) (0, 1, 1)12 was best suited model to predict dengue fever cases [13]. Siregar et al., in their study conducted at Asahan district, North Sumatera Province, Indonesia, also stated that Seasonal ARIMA (0, 0, 1) (0, 1, 1)12 was best suited model for predicting dengue fever cases [12]. P, D, Q values of seasonal part of ARIMA model in the current study results are similar to these two study results. Integration part of ARIMA model i.e. “d” value is similar to these study results. Auto regression part of ARIMA i.e. “p” value is similar to the result study conducted by Promprou et al., who stated that ARIMA (1, 0, 1) was best suited model to predict dengue fever cases in Thailand [22]. Silawan et al., stated that a seasonal ARIMA (2, 1, 0) (0, 1, 1)12 was the best suited model to predict dengue fever cases in North eastern Thailand [23]. P, D, Q values of seasonal part of ARIMA model in this study are similar to the current study results. Mekparyup J et al, stated that a seasonal ARIMA (1, 0, 2) (0, 1, 2)12 was best suited model to predict dengue fever cases in Chonburi, Thailand [24]. Auto regression part of ARIMA i.e. “p” value and “D” value of seasonal part of ARIMA model are similar to the current study results. The differences in the p, d, q values and P, D, Q values of seasonal ARIMA model in different studies might be because of environmental conditions and availability of health care services in those areas.
Forecasted monthly dengue fever incidence from January 2007 to December 2018 was almost nearer to real monthly incidence of dengue fever incidence. The difference between these values may be attributed to the various environmental factors and interventions taken by health care providers.
A Seasonal ARIMA (1, 0, 0) (0, 1, 1)12 was selected as best suited model to predict the future incidence of dengue fever cases in the forthcoming year, which is useful to the health care administrators for better preparedness. The model can be made dynamic to include the current data and correct the model. More complex predictive models could be developed taking into account precipitation, extrinsic incubation period etc. for more accurate prediction. The model can be applied at smaller time frames or geographical levels such as district level to predict the dengue fever incidence.
Copyright:This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.