Review Article - (2025) Volume 14, Issue 2
This study focuses on the practical implementation of Operational Modal Analysis (OMA) with a minimalistic sensor setup, utilizing only a single accelerometer for data acquisition. By employing simulation techniques, the paper explores the identification of eigenfrequencies, a key parameter describing the natural oscillation frequencies of the bridge. This innovative methodology offers valuable insights into the bridge's response to dynamic forces, contributing to a more cost-effective and streamlined approach to structural health monitoring. The paper addresses the inherent challenges and limitations associated with employing a single sensor, showcasing the potential of OMA in scenarios where resource constraints or practical considerations limit the use of multiple sensors. The findings contribute to the broader field of structural dynamics and modal analysis, offering a nuanced perspective on the dynamic characteristics of suspension bridges in real-world conditions.
Eigenfrequencies • Operational modal analysis • Fast fourier transform • Impulse response function • Suspension bridge • Damping ratio
Vibration analysis stands as a cornerstone in the realm of mechanical engineering and structural health monitoring, providing a powerful tool for understanding the dynamic behavior of systems subjected to mechanical oscillations [1-3]. This discipline involves the study and interpretation of vibrational patterns and characteristics within structures or machinery, offering insights into their performance, integrity, and potential issues [4-7].
As mechanical systems and structures continuously experience various forces and external stimuli, they respond with intricate vibrational patterns that carry valuable information about their condition. Vibration analysis, therefore, serves as a diagnostic method to decipher these patterns, enabling engineers and analysts to gain a comprehensive understanding of a system's health, identify potential faults, and optimize its performance [8-11].
Key components of vibration analysis include the study of frequencies, amplitudes, and phase relationships in vibrational signals. These parameters aid in the identification of natural frequencies, resonances, and potential modes of vibration within a system. Furthermore, vibration analysis plays a pivotal role in predictive maintenance strategies, allowing for the early detection of mechanical issues before they escalate into critical failures [12-15].
The methodologies within vibration analysis range from simple manual assessments to sophisticated computational techniques. This field incorporates various sensors, such as accelerometers, to capture vibrational data, and analytical tools, including Fast Fourier Transform (FFT) and modal analysis, to process and interpret this data [16-17].
By understanding the vibrational characteristics of systems, researchers and practitioners can make informed decisions about design, maintenance, and optimization, ultimately contributing to the reliability, safety, and efficiency of mechanical structures and machinery. Through this exploration, we embark on a comprehensive journey into the heart of vibration analysis, unraveling its principles and unveiling its myriad applications in the dynamic landscape of engineering and technology [18-20].
In this study, we delve into the realm of Operational Modal Analysis (OMA) with a keen focus on its practical implementation, emphasizing a minimalist sensor setup. Unlike traditional approaches that often require an array of sensors, our methodology leverages the efficiency of a single accelerometer for comprehensive data acquisition. Through the integration of sophisticated simulation techniques, we embark on a journey to unravel the eigenfrequencies, a pivotal parameter characterizing the natural oscillation frequencies of suspension bridges.
The innovative aspect of this research lies in its commitment to providing valuable insights into the dynamic response of suspension bridges when subjected to varying dynamic forces. We envision a more cost-effective and streamlined approach to structural health monitoring, where the complexity and expenses associated with deploying multiple sensors are minimized. By strategically addressing the challenges and limitations inherently linked to the use of a single sensor, our study serves as a testament to the potential of OMA in scenarios dictated by resource constraints or practical considerations.
As we navigate through the intricacies of our methodology, this paper aims to contribute significantly to the broader field of structural dynamics and modal analysis. By offering a nuanced perspective on the dynamic characteristics of suspension bridges in real-world conditions, our findings not only advance the current understanding of bridge behavior but also pave the way for more efficient and accessible methodologies in structural health monitoring. Through this research, we aspire to bridge the gap between practical constraints and the imperative need for a thorough comprehension of structural dynamics, particularly in the context of suspension bridges.
Eigenfrequency estimation
Eigenfrequency estimation is a crucial step in modal analysis, allowing us to identify the natural frequencies at which a structure vibrates. In this study, the initial estimates of eigenfrequencies are obtained using the classical peak-picking method. Let's break down this process in detail:
Frequency domain representation: The first step involves transforming the time-domain data into the frequency domain. This is typically done using techniques such as the Fourier transform. The result is a frequency spectrum showing different frequencies' contribution to the overall signal.
Identification of peaks: The classical peak-picking method is employed to identify prominent peaks in the frequency spectrum. Peaks represent specific frequencies at which the structure vibrates. These frequencies are associated with the eigenmodes of the structure.
Peak detection algorithm: Various algorithms can be used for peak detection, and the choice depends on the characteristics of the data. Common algorithms include threshold-based methods, derivative based methods, or more advanced techniques like wavelet analysis.
Threshold setting: A threshold may be set to distinguish significant peaks from noise. Peaks above the threshold are considered valid eigenfrequencies, while smaller peaks are ignored.
Eigenfrequency extraction: Once the peaks are identified, the corresponding frequencies are extracted. These frequencies represent the initial estimates of the eigenfrequencies of the structure.
Significance of eigenfrequencies: Eigenfrequencies are fundamental to the dynamic behavior of a structure. They indicate the rates at which the structure naturally vibrates in different modes. The goal is to accurately identify these frequencies to gain insights into the structural response under various conditions.
Iterative refinement: It's important to note that initial eigenfrequency estimates may undergo further refinement through iterative processes. Refinement techniques, such as curve fitting or advanced modal identification algorithms, may be applied to improve the accuracy of the estimates.
Validation and comparison: The final set of eigenfrequencies obtained through this process is then compared with the target eigenfrequencies or those obtained through other means (e.g. numerical simulations). This validation step ensures the reliability of the estimated eigenfrequencies.
The classical peak-picking method provides a straightforward and effective way to obtain initial estimates of eigenfrequencies from experimental or simulated data. Subsequent steps in the modal analysis process, such as mode shape identification and damping ratio estimation, often build upon these initial eigenfrequency estimates to comprehensively characterize the dynamic behavior of the structure (Figure 1).
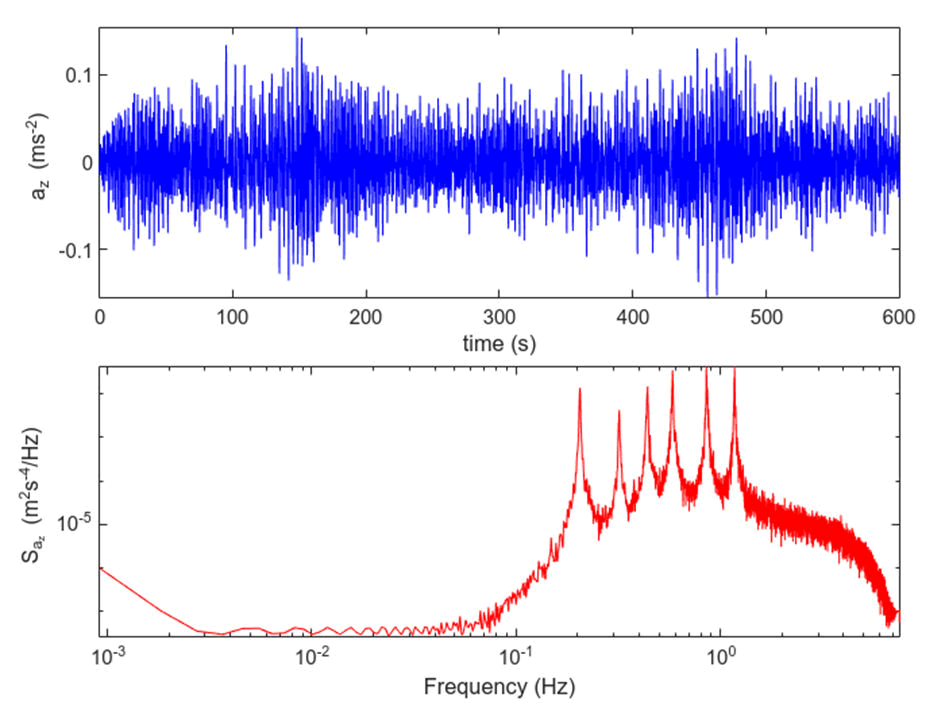
Figure 1. Eigenfrequency estimation.
Automated peak-picking method
An automated peak-picking method refers to a computational approach or algorithm designed to identify and extract prominent peaks from a dataset, such as a signal or a spectrum. This method is commonly used in various fields, including signal processing, spectroscopy, chromatography, and data analysis. The goal is to automate the process of detecting significant peaks within a dataset, saving time and ensuring consistency in peak identification (Figure 2).
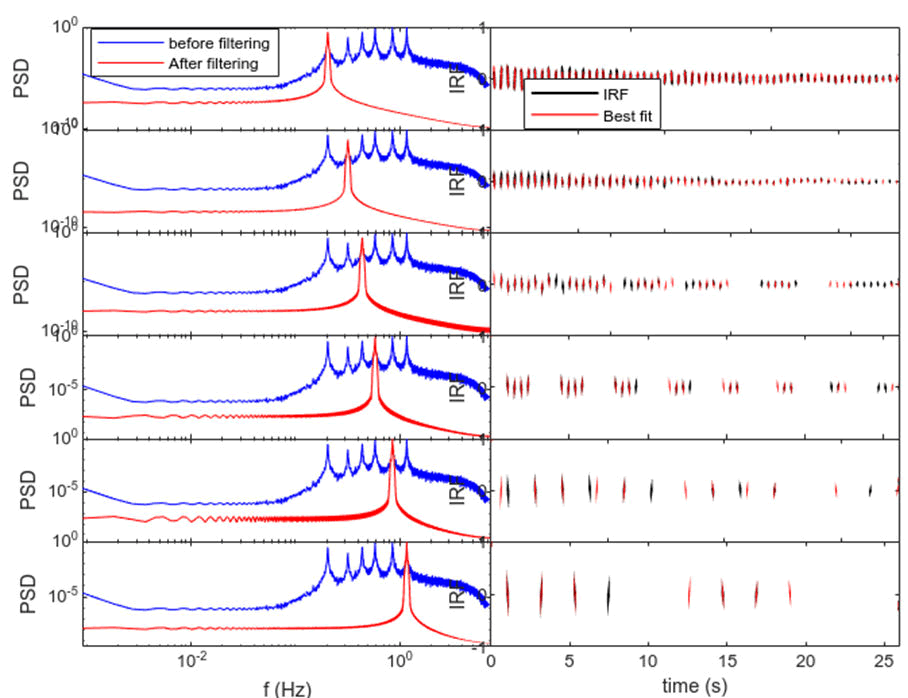
Figure 2. The adequacy of the filtering and fitting.
Automated peak-picking methods play a crucial role in high throughput data analysis, where manual identification of peaks may be impractical. These methods are applied in a variety of scientific and industrial contexts, providing efficient and consistent peak identification in large datasets. The choice of a specific method may depend on the nature of the data, the characteristics of the peaks, and the user's specific requirements.
Damping ratio estimation
In the study of dynamic systems and structural vibrations, the estimation of damping ratios plays a crucial role in understanding how a system dissipates energy over time. This estimation becomes particularly relevant when analyzing the response of structures to external forces, such as those experienced by bridges, buildings, or mechanical components. One common method employed for damping ratio estimation involves fitting an exponential decay function to the Impulse Response Function (IRF) of the system.
Our focus is on the application of damping ratio estimation through the fitting of an exponential decay function to the IRF. The impulse response function represents the system's response to an impulse, providing valuable information about its dynamic behavior. By modeling the decay of the response with an exponential function, we can extract critical parameters, specifically the damping ratios associated with the identified eigenfrequencies.
The fitting process allows us to quantify how quickly the vibrations within the system decay after an external force is applied. A higher damping ratio indicates a faster decay, signifying a system that dissipates energy more rapidly. Conversely, a lower damping ratio suggests a slower decay, indicating a system with greater capacity to sustain oscillations.
Introduction to manual peak-picking method
In the realm of signal processing and data analysis, the manual peak-picking method stands as a traditional yet valuable approach for identifying significant peaks within datasets. Unlike automated algorithms, which employ computational techniques to identify peaks, the manual method involves human intervention to visually inspect and select peaks of interest. This hands-on approach allows analysts to carefully scrutinize the data, taking into account domain specific knowledge and subjective judgment.
In this study, we delve into the nuances of the manual peak picking method, recognizing its historical significance and enduring relevance in various scientific disciplines. By leveraging the expertise of human analysts, this method enables a qualitative and context aware identification of peaks, which may be crucial in scenarios where the data's complexity or uniqueness demands a more tailored and nuanced approach (Figure 3).
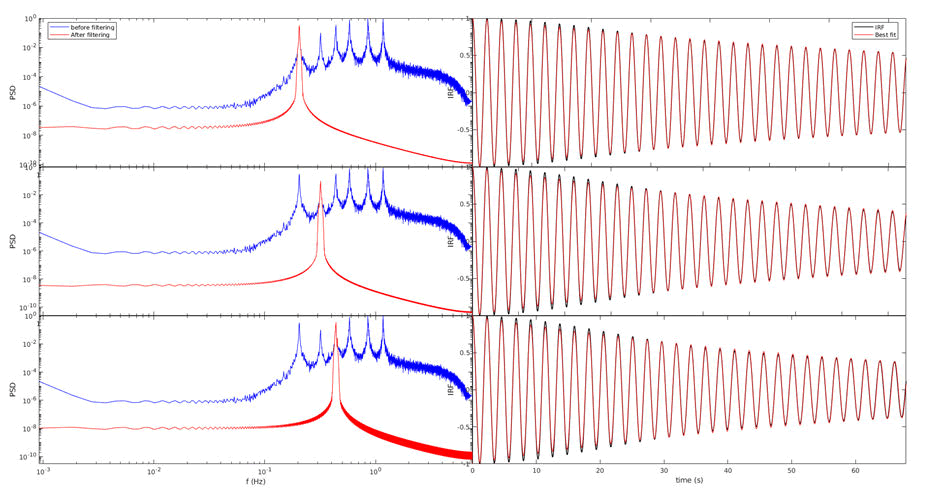
Figure 3: Manual peak-picking method.
Throughout this exploration, we will discuss the intricacies of the manual peak-picking process, shedding light on the factors influencing peak selection, such as peak height, width, and overall shape. We will also examine the advantages and challenges associated with manual peak picking, considering its applications in fields such as spectroscopy, chromatography, and signal processing.
As we navigate the landscape of manual peak picking, we aim to provide a comprehensive understanding of its principles, methodologies, and potential implications for data analysis. By doing so, we contribute to the broader discourse on peak identification methods, recognizing that the manual approach, despite its inherently subjective nature, remains an invaluable tool in the hands of skilled analysts and researchers. Through this exploration, we hope to provide insights that inform the ongoing dialogue between traditional manual methods and emerging automated techniques in the ever-evolving landscape of data analysis and scientific inquiry.
The primary goal of the described methodology is to identify two important dynamic parameters of the suspension bridge: Eigenfrequency and damping ratio. These parameters provide insights into how the bridge responds to dynamic loads, such as those experienced under ambient loading conditions. The described methodology provides a practical approach to eigenfrequency and damping ratio identification for a suspension bridge using only a single accelerometer. The simulation and analysis contribute valuable insights into the dynamic behavior of the bridge under ambient loading conditions. This approach, while having limitations, demonstrates the potential of OMA with a single sensor in certain scenarios.
Received: 02-Jan-2024, Manuscript No. JBTW-24-124327; Editor assigned: 04-Jan-2024, Pre QC No. JBTW-24-124327 (PQ); Reviewed: 18-Jan-2024, QC No. JBTW-24-124327; Revised: 21-Mar-2025, Manuscript No. JBTW-24-124327 (R); Published: 28-Mar-2025, DOI: 10.35248/2322-3308.25.14(2).001
Copyright:This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.